I welcome supervision inquiries from motivated students and young researchers at all levels. To ensure I can dedicate the proper time and provide high-quality guidance to every candidate, I am unfortunately not able to accommodate all the requests I receive.
I have several projects currently available, and I encourage students to propose their own as well. For more information or to schedule a meeting, please get in touch via email.
See below for some practical details about thesis projects.
Final project (LT)
A final project in mathematical analysis of course requires a good background and interest in the area. This is an excellent opportunity to dive deeper into a topic from a previous course, explore a new subject of interest, or even get an early start on advanced material.
Rather than vaguely covering a broad piece of mathematical landscape, it is arguably better to prioritize here depth over breadth and develop expertise in a narrow, focused topic. This involves organizing your self-study to achieve a deep understanding – by consulting several sources, doing exercises, detailing proofs and examples, and performing explicit computations.
The final project is usually worth 3 CFU, which is formally 75 hours of work. Developing the project and writing a short essay typically takes around four months, but this timeline can vary significantly based on your course load and how in-depth you want to go. A good rule of thumb is to make arrangements about six months before your desired graduation date.
While the topic itself is important, in my opinion the primary goal of a bachelor’s thesis is to develop the following key skills:
- Practice scientific writing. The final project is likely your first chance to write a scientific text from scratch. This requires a significant effort that involves learning to find and cite sources, develop a bibliography and structure a coherent essay. You can even choose to write it in English for an extra challenge.
- Practice scientific communication. The oral defense of your project is an excellent exercise in presenting a mathematical topic clearly and concisely within a strict time limit. These constraints will force you to identify the most important aspects of your work and deliver them in an engaging way.
- Practice scientific drafting. All professional mathematical texts are typeset using some form of LaTeX nowadays. Your final project is a good occasion to learn the basics of LaTeX, which is especially useful if you plan to continue your studies in this field. See the “Learn LaTeX in 30 minutes” tutorial for a quick introduction.
Master thesis (LM)
The choice of a master’s thesis topic is very important. At this stage, students are expected to have the scientific maturity of a young scholar with good general knowledge of their discipline and a clear direction toward a specialization. For this reason, your thesis topic should align your interests with the research areas of your supervisor. In this case, we can decide on a suitable subject after discussing your preferences and inclinations.
In addition to basic skills in scientific writing (in English) and LaTeX, you will need a good command of basic mathematical analysis, from calculus to functional analysis. Depending on the project, you may also need to have taken courses in more advanced subjects (e.g., courses in Fourier analysis, quantum mechanics, signal processing, statistical learning).
My thesis proposals generally revolve around literature reviews of advanced topics. Note that a significant effort is required to absorb the necessary background material before being able to tackle research articles. However, depending on the available time and the student’s maturity, both theoretical and application-oriented original research projects may be offered as well, possibly with computational components.
The master’s thesis is typically worth 16 CFU, which is formally equivalent to 400 hours of work, and involves writing a long scientific report. To be safe, I recommend making arrangements about eight months before your target graduation session. Regular meetings for discussion and supervision are offered based on the student’s needs. In any case, students are expected to be fairly diligent and independent, and take responsibility for their project’s progress.
PhD candidates
Prospective PhD students are encouraged to contact me via email to discuss potential research projects and opportunities. See my publications for recent research problems.
Please be aware that admissions to the PhD programs at Politecnico di Torino take place twice a year through public competitions. The selection process is handled at the department level by appointed committees.
Beyond Politecnico
While my thesis proposals are primarily targeted to students of math/phys-oriented degrees at Politecnico di Torino, I am always open to co-supervise BSc/MSc/PhD students from other universities and/or diverse degree programs.
If you are an external student and our research interests align, please feel free to reach out.
A list of recent thesis projects
Master
- 2025 – Eugenio Del Nero – Università degli Studi di Torino, Mathematics (LM-40)
Expressivity of Neural Networks - 2024 – Claudio Fantasia – PoliTO, Data Science and Engineering (LM-32)
Patch-based Learning of Space-variant Hyperparameters in Variational Image Restoration - 2024 – Vitória Dos Anjos – Università degli Studi di Torino, Mathematics (LM-40)
Aspects of Geometric Learning with Convolutional Neural Networks - 2023 – Cristina Febbraiola – PoliTO, Mathematical Engineering (LM-44)
Time-Frequency Analysis and Localization Operators
Bachelor
- 2024 – Alessandro Falcone – PoliTO, Mathematics for Engineering (L-35)
Topics: the Radon transform and applications - 2024 – Giorgia Malfeo – PoliTO, Mathematics for Engineering (L-35)
Topics: basics of quantum dynamics and the Schrödinger equation - 2024 – Alberto Spinello – PoliTO, Mathematics for Engineering (L-35)
Topics: aspects of high-dimensional Euclidean spaces - 2023 – Valerio Taralli – PoliTO, Mathematics for Engineering (L-35)
Topics: mathematical structure of convolutional neural networks - 2023 – Alessandro Di Grazia – PoliTO, Mathematics for Engineering (L-35)
Topics: uncertainty principles in quantum mechanics and Fourier analysis
Here is an informal outline of my research areas, which can serve as starting point for further reading and exploring possible thesis topics – follow the links!
Harmonic analysis in phase space

In 2022 we celebrated the bicentennial of the publication of Fourier’s Théorie analytique de la chaleur. In this seminal work he solved the heat equation by leveraging the visionary idea that any function can be viewed as the superposition of sinusoids. Modern Fourier analysis continues to build upon this insight, but nowadays sinusoids are replaced by different dictionaries of elementary signals.
The ultimate goal is to perform a joint time-frequency analysis of a function/distribution. However, it turns out that time and frequency have a dual nature – two faces of the same coin, and trying to keep an eye on both faces at the same time is hampered by the diverse manifestations of the uncertainty principle.

This research area naturally interlaces several branches of modern analysis. Some aspects I am interested in:
Time-frequency and multiscale analysis. We decompose functions and distributions into elementary wave packets in terms of Gabor atoms, wavelets, shearlets, etc. In short, this is the mathematical theory of signal processing, and also provides a powerful approach to study the key features of more general operators and PDEs.
Microlocal and semiclassical analysis. In a nutshell, they provide a rigorous framework for understanding the high-frequency behavior and the short-wavelength limits of oscillatory models. Tools like wave front sets are introduced to detect the location and nature of singularities in solutions to PDEs.
Function spaces of harmonic analysis. In order to deal with time and frequency/scale jointly, several ad hoc function spaces are introduced – such as Sobolev, Besov, modulation and amalgam spaces. Understanding the properties of these spaces is crucial for many purposes, including well-posedness of PDEs or discrete approximation algorithms.

Localization in phase space and uncertainty principles. Informally, the uncertainty principle is a metatheorem that states that a signal cannot be perfectly localized in both time and frequency. We explore in a quantitative way the many facets of this issue, as it poses significant challenges in signal processing and quantum mechanics.
Mathematical aspects of quantum physics

We investigate problems of quantum theory through a rigorous mathematical lens, using a wide array of techniques from functional analysis, spectral theory and operator algebras. This approach is closely related to phase space analysis, since several pairs of physical quantities (like position and momentum) share a dual nature similar to that of time and frequency.
Here are some topics I am particularly interested in.
Quantization and pseudodifferential calculus. This area explores the relationship between classical and quantum observables, in order to make a rigorous transition from the commutative world of functions on phase space to the non-commutative realm of operators in quantum mechanics, using different quantization rules and related calculi.
Operators and PDEs in mathematical physics. We study the properties of solutions to key equations in QM such as the Schrödinger, Dirac, and Klein-Gordon equations. We also analyze the regularity and time evolution of these solutions, as well as distinctive phenomena and the spectral properties of their associated quantum Hamiltonians.
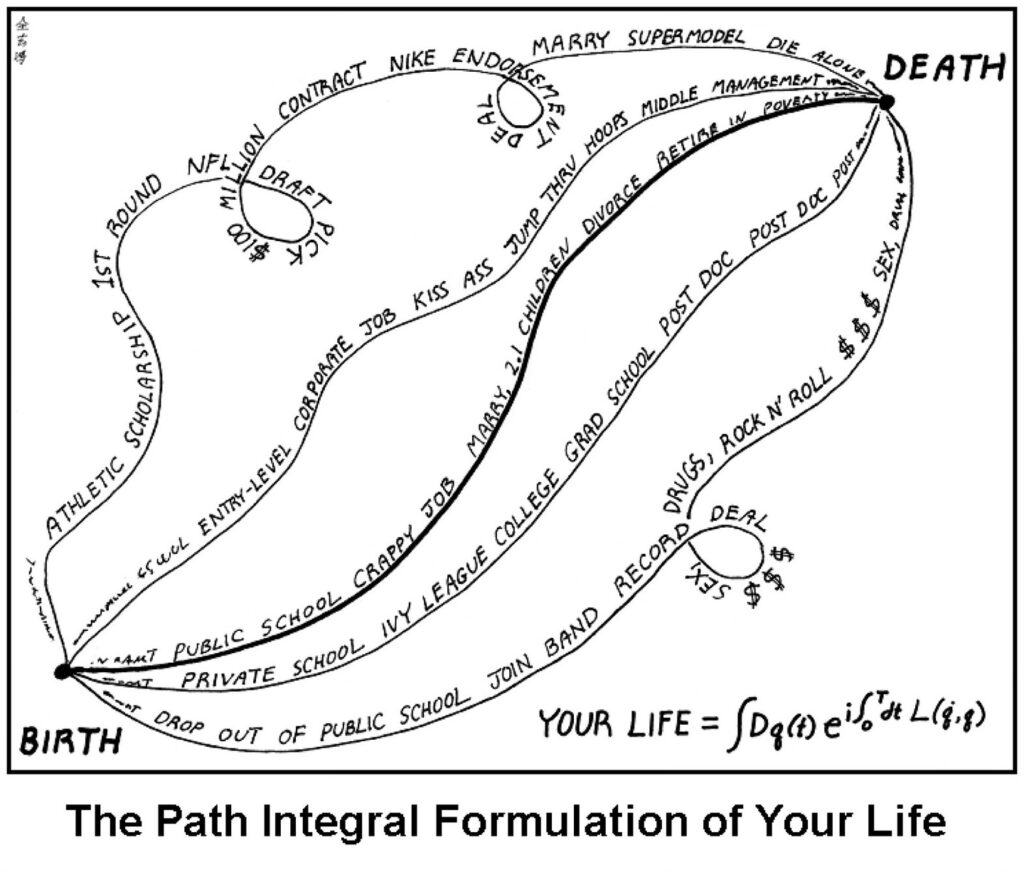
Rigorous Feynman path integrals. This involves making Feynman’s (very effective!) heuristics of quantum dynamics – that a system’s behavior arises from a weighted virtual exploration of all its possible histories – mathematically sound, which still remains a largely open challenge.
Quantum information. As quantum computing becomes more tangible, there is a growing need for a rigorous understanding of information theory. We explore mathematical results related to concepts like entanglement, quantum channels and entropy.

Applied and computational harmonic analysis
This dynamic field entails leveraging theoretical principles from harmonic analysis to design powerful approaches for tackling real-world challenges in data science and signal processing. Different types of signals, from sounds to images, are variously represented using tools of approximation theory such as expansions with respect to bases and frames.
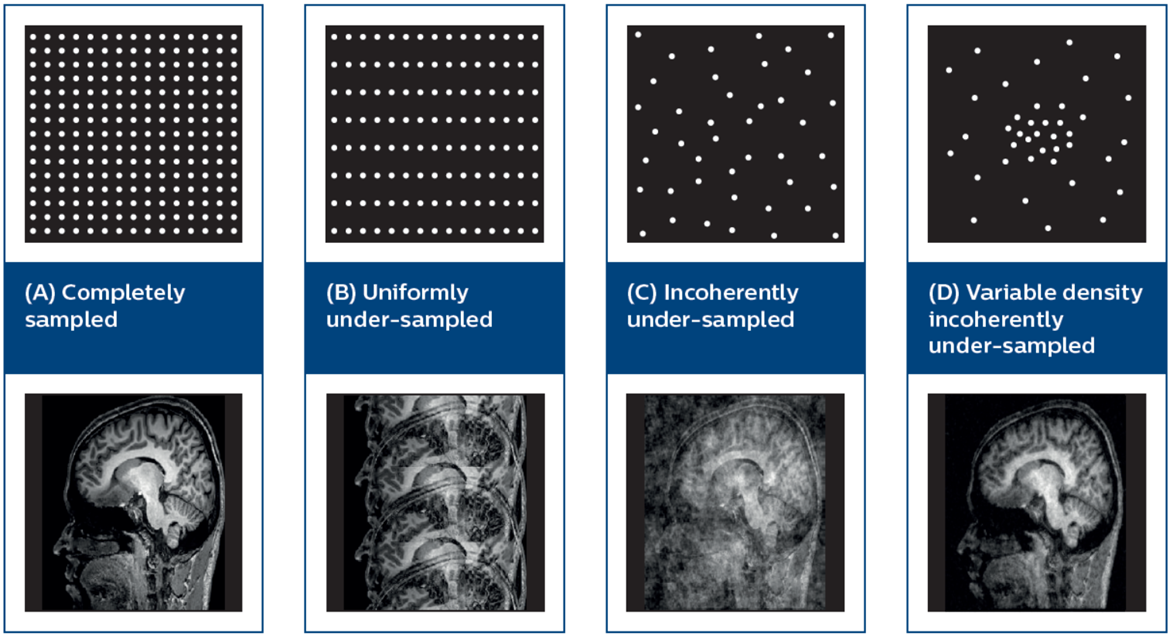
A key concept is sparsity, which refers to representations with a limited number of significant coefficients. This is the main thrust of compressive sensing, which allows for accurate reconstruction of signals and images from surprisingly few measurements, and has already had a significant impact on diverse fields like medical imaging, non-destructive testing and astronomy.
More generally, we address inverse problems in imaging and PDEs, where the goal is to accurately recover a quantity of interest from indirect, noisy measurements. We use mathematical tools to design and ensure robustness and efficiency of reconstruction procedures.

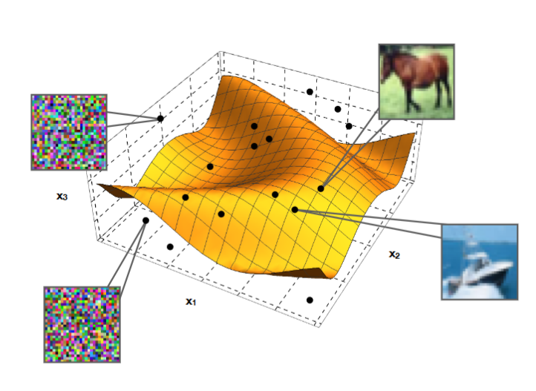
Recent applications of harmonic analysis ideas can be found in the mathematics of data science. Specifically, the analysis of deep learning models like convolutional neural networks, the geometry of data manifolds, geometric learning on non-Euclidean domains (e.g., graphs) and in high-dimensional spaces are challenges that can greatly benefit from the powerful lens of Fourier analysis.
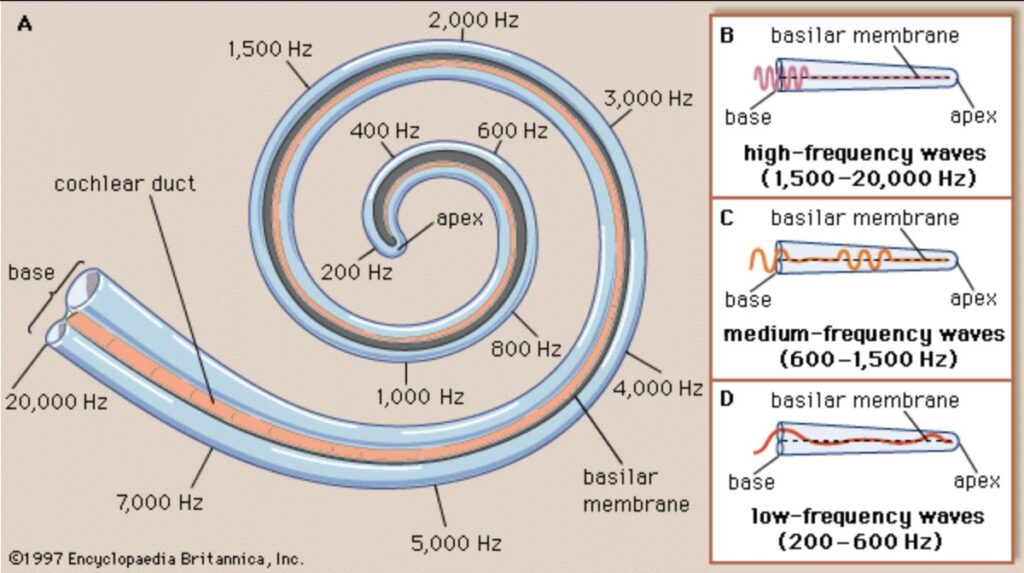
To conclude, we mention that multiscale analysis is the mathematical language of perception, providing tools and models for the neurophysiology of vision and hearing. Indeed, wavelet filters help us understand how the visual cortex breaks down images into basic features like edges. Moreover, it turns out that our auditory system inherently performs multiresolution analysis.